Série de FOURIER
Un signal f(t) périodique de période T peut s'exprimer sous la forme d'une somme infinie de sinus et cosinus :
\(\boxed{f(t) = a_0 + \sum_{n=1}^{\infty} (a_n . cos( \frac{2\pi n}{T}t) + b_n . sin( \frac{2\pi n}{T}t))}\)
\(a_0=\frac{1}{T}\LARGE\int_{\normalsize -T/2}^{\normalsize T/2}\normalsize f(t) dt~~(=valeur~moyenne)\)
\(a_n=\frac{2}{T}\LARGE\int_{\normalsize -T/2}^{\normalsize T/2}\normalsize f(t) cos( \frac{2\pi n}{T}t)dt\)
\(b_n=\frac{2}{T}\LARGE\int_{\normalsize -T/2}^{\normalsize T/2}\normalsize f(t) sin( \frac{2\pi n}{T}t)dt\)
Simplifications
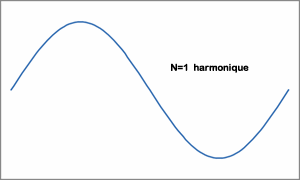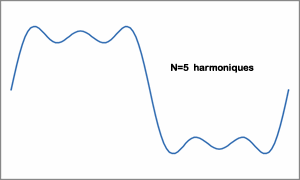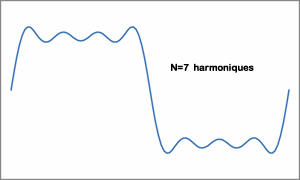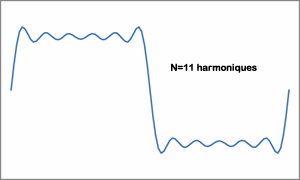
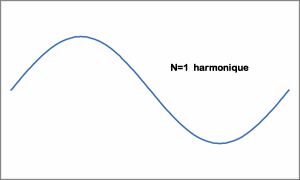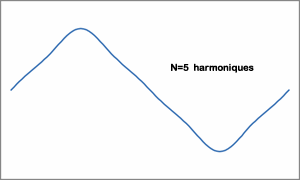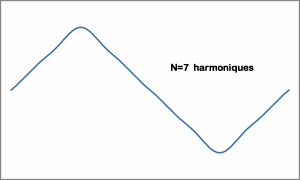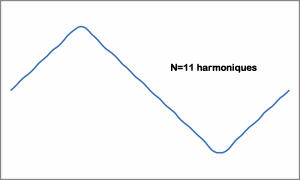
En pratique, on arrête n à une valeur finie, plus n est élevé, plus le signal reconstitué sera fidèle à l'original.
Si le signal possède une parité paire, les coefficients bn seront tous nuls, il n'y aura que des coefficients an (cosinus)
Si le signal possède une parité impaire, les coefficients an seront tous nuls, il n'y aura que des coefficients bn (sinus)
Si le signal présente une symétrie par rapport à la demi-période, il n'y aura que des coefficients impairs